Softmax Regression

개요

기본적인 선형 회귀 함수 형태인 $H_L(x) = Wx$ 의 return 값은 [100, 200, -100] 과 같은 실수로 이루어져있다. 하지만 우리가 원하는 것은 Binary (1, 0)을 분류하는 목적엔 적합하지 않다.

그래서 $H_L(x) = z$ 로 대체하여 실수 값인 $z$를 1과 0 사이의 값으로 압축하는 새로운 함수인 $g(z)$를 활용한다. 그것이 바로 이전 포스팅에서 공부했던 sigmoid function 이다.

즉 최종적인 hyphothesis는 $H_R(x) = g(H_L(x))$로 표현할 수 있다. 해당 과정을 그림으로 간략히 표현하면 아래와 같다.

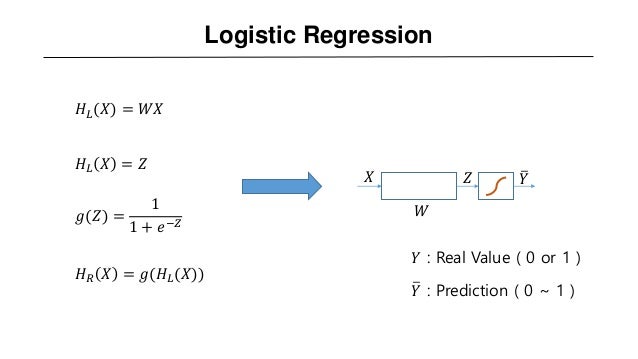
앞선 로지스틱 회귀를 통해 2개의 선택지 중에서 1개를 고르는 이진 분류(Binary Classification)을 확인했고 이제는 3개 이상의 선택 중에서 1개를 고르는 다중 클래스 분류를 위한 소트프맥스 회귀(Softmax Regression)에 대해서 공부해보자

Step 2. 다중 클래스 분류(Multi-class Classification)

기존에 범주가 2개였던 경우에는 각각의 범주에 속하는지 아닌지 판단하는 hyperplane 하나를 설정하면 됐다. 그러나 3개가 되는 경우에는 갑자기 3개로 늘어났다.

해당 그래프를 그림으로 다시 표현해보면 input $x$에 대해 weight $W$를 곱해주고 나온 결과를 다시 sigmoid 함수를 통해 결과 값을 얻는다. 각 class 마다 자신의 weight vector가 존재하기에 출력 결과도 독립적일 것이다.

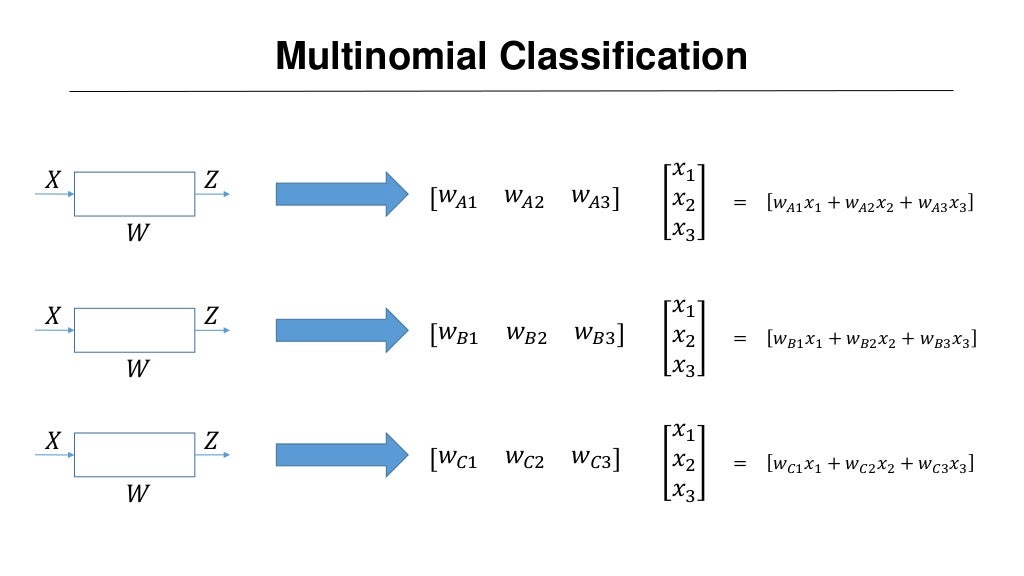
각 weight vector를 하나의 matrix로 합치게 되면 다음과 같이 표현이 가능하다.

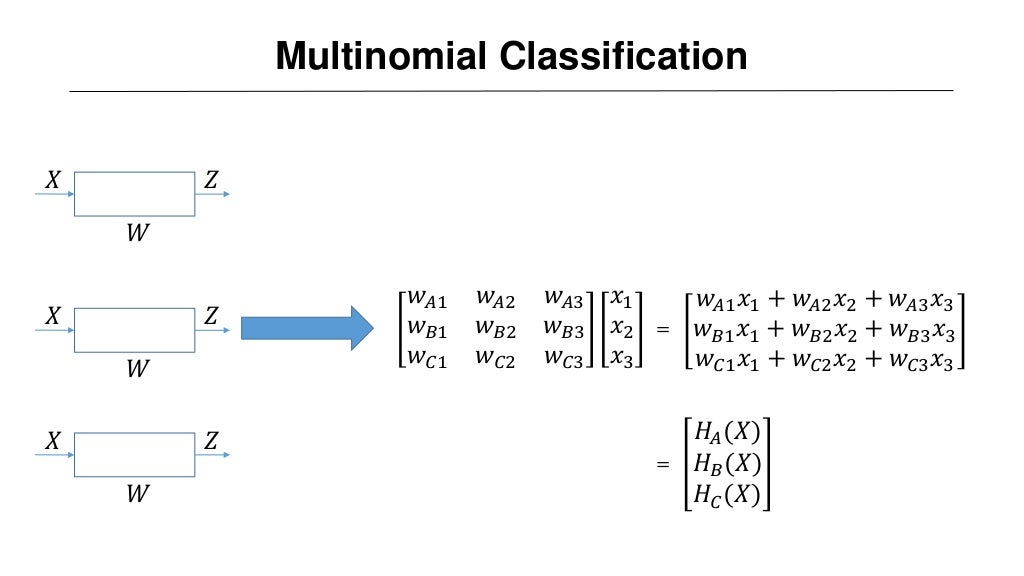
가중치가 계산된 최종 출력값을 sigomoid 함수를 통해 계산하게 된다면 0~1 사이의 값들이 나오게 된다. 그러나 A = 0.6, B = 0.61, C = 0.612 로 산출된다면 어느 범주를 선택해할지 애매하게 된다.

만약 각 범주의 확률의 총 합이 1인 확률 분포를 구할 수 있게 되면 어떨까? 그렇다면 각 범주의 산출된 확률끼리 비교할시 훨씬 용이하게 된다.

이럴 때 사용할 수 있는 것이 소프트맥스 함수이다.

Step 3. 소프트맥스 함수(Softmax Function)

소프트맥스 함수는 분류해야하는 범주의 총 개수를 k라고 할 때, k 차원의 벡터를 입력받아 각 범주에 대한 확률을 추정한다.

1) 소프트맥스 함수의 이해

k차원의 벡터에서 i번째 원소를 $z_i$, i번째 클래스가 정답일 확률을 $p_i$로 나타낸다 하였을 때 소프트맥스 함수는 $p_i$를 다음과 같이 정의한다.

$p_{i}=\frac{e^{z_{i}}}{\sum_{j=1}^{k} e^{z_{j}}}\ \ for\ i=1, 2, … k$

그렇담 위의 예시를 소프트맥스 함수에 적용 시킨다면

$softmax(z)=[\frac{e^{z_{1}}}{\sum_{j=1}^{3} e^{z_{j}}}\ \frac{e^{z_{2}}}{\sum_{j=1}^{3} e^{z_{j}}}\ \frac{e^{z_{3}}}{\sum_{j=1}^{3} e^{z_{j}}}] = [p_{1}, p_{2}, p_{3}] = [p_{A}, p_{B}, p_{C}]$

와 같이 수식을 표현할 수 있다. 결과를 예시로 들어보면 $p_{A}$ = 0.6, $p_{B}$ = 0.1, $p_{C}$ = 0.3 로 모든 확률의 총 합은 1인 확률로 표현이 가능하다.

즉, 아래 그림과 같이 요약을 할 수 있다.

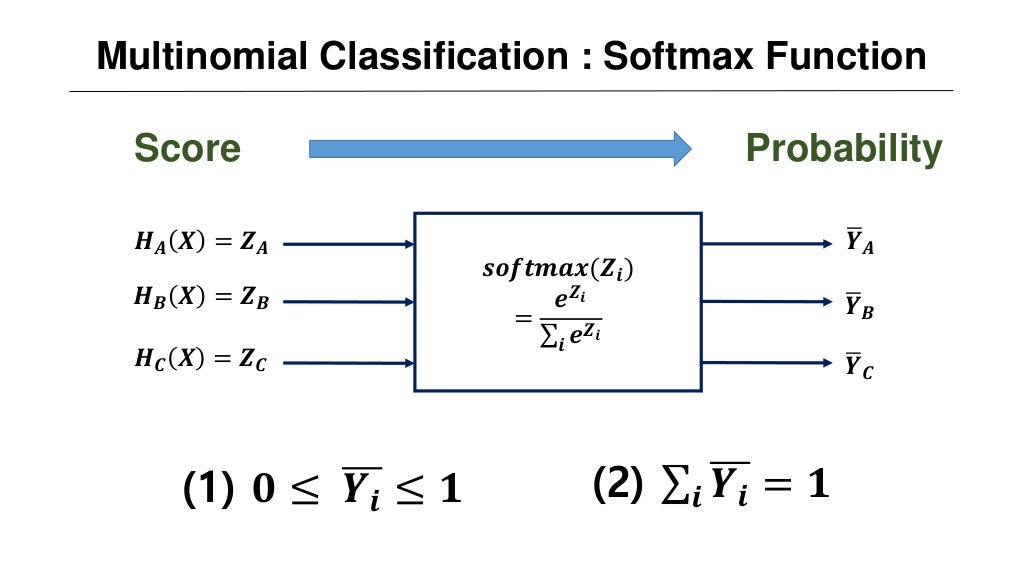
그럼 소프트맥스 함수를 통해서 나온 각 범주에 대한 예측값 [0.6, 0.1, 0.3] 과 비교할 수 있는 실제값은 one-hot vector로 표현을 한다.

예를 들면 A가 실제 정답이라면 [1,0,0], B가 실제 정답이라면 [0,1,0]과 같이 표현을 한다.

A가 정답인 경우 예측값과 실제값의 오차가 0이 되는 경우는 소프트맥스 함수의 결과가 [0,1,0]이 되는 경우이다. 이 두 벡터의 오차를 계산하기 위해 cost function으로 크로스 엔트로피 함수 를 이용한다.

Step 4. 비용 함수 (Cost Function)

softmax regression에서는 비용 함수로 크로스 엔트로피 함수를 이용한다.

1) 크로스 엔트로피 함수

밑의 수식에서 $y$는 실제값을 나타내며, $k$는 클래스의 개수로 정의한다. $y_j$는 실제 one-hot vector의 $j$번째 인덱스를 의미하며, $p_j$는 샘플 데이터가 $j$번째 클래스일 확률을 나타낸다. 즉 위에서 살펴보았던 소프트맥스로 산출된 확률 값이다. 표기에 따라서 $\hat{y}_{j}$로 표현하기도 한다.

$cost(W) = -\sum_{j=1}^{k}y_{j}\ log(p_{j})$

해당 함수를 다르게 조금만 다르게 표현해볼까?

$cost(W) = \sum_{j=1}^{k}y_{j}(-\ log(p_{j}))$

어디서 많이 본 모양이다. 그렇다 앞서 공부했던 logitic의 cost function의 모양과 비슷하다.

그럼 간단한 경우로 그림으로 표현해보면

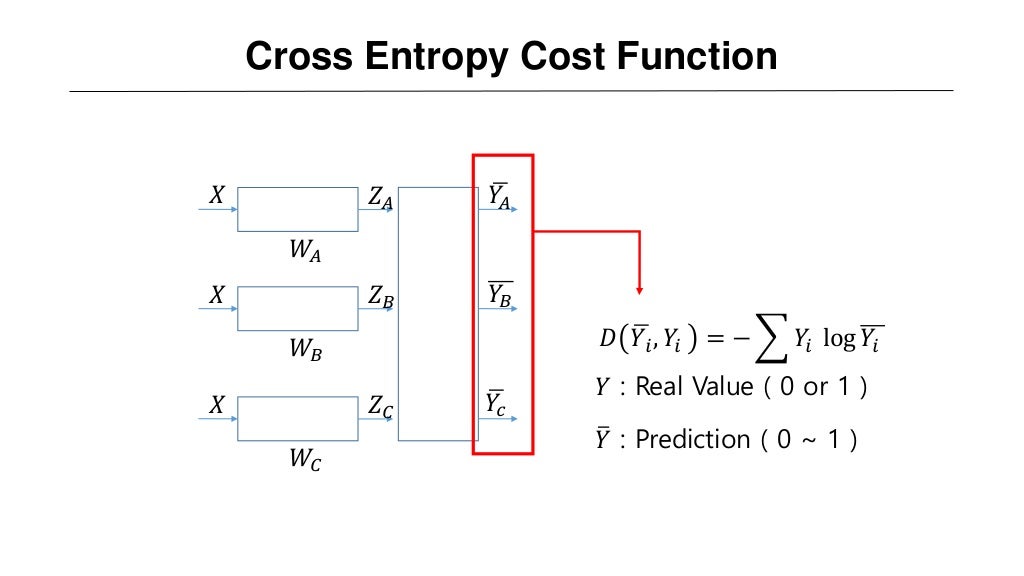
$Y_i = y_j$, $\hat{Y}_{i} = p_j$ 로 대체하면 위와 같이 표현이 가능하다.

직관적인 이해를 위해서 실제값이 [1,0,0]인 경우 예측값을 [1,0,0] 로 표현하면 Cross entropy의 연산 과정을 아래와 같이 볼 수 있다.

즉 실제값과 예측값이 정확이 일치하게 된다면 해당 cost function의 값은 0이 된다. 그러나 그렇지 않은 경우엔 cost function의 값이 무한으로 발산하는 값이 된다.

즉 $D(\hat{Y}_i, Y_i)$ 의 값을 최소화하는 방향으로 학습을 해야하며 이제 이를 n개의 전체 데이터에 대한 평균을 구하면 최종 비용함수는 다음과 같다.

$Cost(W) = \frac{1}{N}\sum_nD_n(\hat{Y}, Y) = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{k}y_{j}^{(i)}\ log(p_{j}^{(i)})$

참고 자료

[https://wikidocs.net/35476] [http://hleecaster.com/ml-linear-regression-concept/]

https://www.slideshare.net/ssusereab2f3/multinomial-classification-amp-application-of-ml

https://hunkim.github.io/ml/

소프트맥스 회귀 공부