Gradient descent algorithm 사용시 주의점
목차
- Step 1. 개요
- Step 2. 학습률(Learning Rate)
- Step 3. 피쳐 스케일링(Feature Scaling)
해당 게시물은 참고자료를 참고하거나 변형하여 작성하였습니다.
Step 1. 개요
앞선 포스팅에서 머신러닝, 딥러닝 학습은 결국 모두 Cost function을 최소화 하는 parameter들을 찾는 것이 목적이며 이때 사용되는 알고리즘을 Optimizer or 최적화 알고리즘이라 칭한다고 했다.
Optimizer를 통해서 해당 parameter들을 찾는 과정을 학습(training)이며 따라서 반복을 최소화 하면서 학습 시간을 줄이며 빠르게 parameter를 찾는 것이 매우 중요하다. 실제로 알고리즘을 돌릴 때 유의할 점 들이다.
그 중에 선형회귀에서 쓰인 가장 기본적인 optimizer인 경사 하강법(Gradient Descent) 을 사용할 시 유의할 점에 대해 공부해보자.
Step 2. 학습률(Learning Rate)
경사 하강법(gradient descent)에 원리는 비용 함수를 미분하여 현재 $W$에서의 접선의 기울기를 구하고, 접선의 기울기가 낮은 방향으로 $W$의 값을 변경하고 다시 미분하는 과정을 반복한다.
즉 위의 그림과 같이 접선의 기울기가 0이 되는 지점, 또한 미분값이 0이 되는 지점을 cost가 최소화 되는 지점을 향해 학습을 하는 것이다.
$W := W - α\frac{∂}{∂W}cost(W)$
이렇게 현재값과 접선의 기울기를 빼서 새로운 $W$를 갱신하며 최적의 $W$를 찾아간다 . 공식을 살펴보면 $α$가 보이는데 이것이 바로 학습률(learning rate) 이다.
1) learning rate 의미
learning rate alpha는 알고리즘이 동작하는 속도를 결정한다. 간단하게 예를들면 우리가 등산을 할 때 목표 지점으로 향하면서 보폭을 얼마나 걸으며 움직이는 것이냐는 것이다. 머신러닝, 딥러닝에서는 learning rate의 설정이 매우 중요하다.
2) learning rate이 큰 경우
해당 경우에는 overshooting 현상이 나타날 수 있다. 아래의 그림으로 확인해보자.
정상적이라면 경사를 따라 내려가면서 최소지점에 도달하여 cost의 최소값을 얻을 수 있어야 한다.
하지만 learning rate가 너무 크면, 최솟값을 찾지 못하고 이리저리 왔다갔다하며 cost value 가 발산하는 경우가 생긴다.
즉, cost 를 최소화 하는 함수에 있어서 cost가 줄어들지 않고 오히려 점점 늘어나는 현상이 있다면 learning rate가 너무 큰게 아닌지 의심해야 한다.
3) learning rate이 작은 경우
위 경우에는 아래와 같이 너무 학습시간이 오래걸리며, 최적해가 아닌 지역 최적해에서 멈춰버리는 수가 있다.
안타깝게도 한번에 최적의 learning rate를 찾는 방법은 없기에 cost의 변화량을 보며 learning rate를 조절해야 한다. 보통 0.01 로 설정하여 조금씩 늘려가는 방법을 사용한다고 한다.
Step 3. 피쳐 스케일링(Feature Scaling)
Feature scaling 이란 데이터의 독립 변수 또는 피처의 범위를 정규화하는 데 사용되는 방법이다. 일반적으로 전처리 과정에서 행한다.
해당 과정을 거치는 이유는 각각의 Feature, 즉 변수마다 측정단위가 다를 것이고, 범위도 모두 상이하다.
학습 데이타의 각 Feature의 값이 범위가 크게 차이가 나면 머신러닝 학습이 잘 안되는 경우가 존재한다. 예를 들어 속성 A(나이)의 범위가 0 ~ 100이고, 속성 B(재산)의 범위가 0~100000000 이면, 학습이 제대로 되지 않을 수 있다.
그래서 각 속성의 값의 범위를 동일하게 맞추는 것을 스케일링 (Feature scaling) 과정이 필요하다.
Feature scaling의 대표적인 두 가지 방법에 대해 공부해보자.
1) 최소- 최대 정규화(Min-Max Normalization)
데이터의 최소값, 최대값을 알 경우에 사용하며 일반적으로 0~1 사이의 값으로 변환시켜준다.
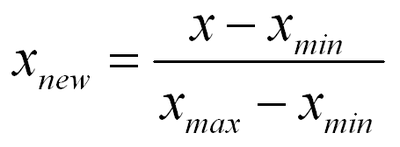
2) 표준화(Standardization)
평균을 기준으로 얼마나 떨어져 있는지를 나타내는 값으로, 기존 변수에 범위를 정규 분포로 변환한다.
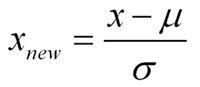
참고자료
https://hunkim.github.io/ml/ https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-8-Feature-Scaling-Feature-Selection


