과적합(Overfitting) 방지
목차
- Step 1. 과적합(Overfitting) 정의
- Step 2. 해결책
- Step 2.1 데이터 셋 늘리기
- Step 2.2 Feature 개수 줄이기
- Step 2.3 가중치 Regularization(규제화)
해당 게시물은 참고자료를 참고하거나 변형하여 작성하였습니다.
Step 1. 과적합(Overfitting) 정의
Overfitting
통계나 머신 러닝에서 사용되는 용어로서, 제한된 샘플(data)에 너무 특화되어 새로운 샘플(data)에 대한 예측 결과가 오히려 나빠지거나 학습의 효과가 나타나지 않는 경우이다.
즉 모델에 특정 training data를 과하게 학습을 시키면, 그 모델은 해당 training data에 좋은 성능을 보이지만, 새로운 test data에 대해서는 좋지 않는 성능을 나타내게 된다.
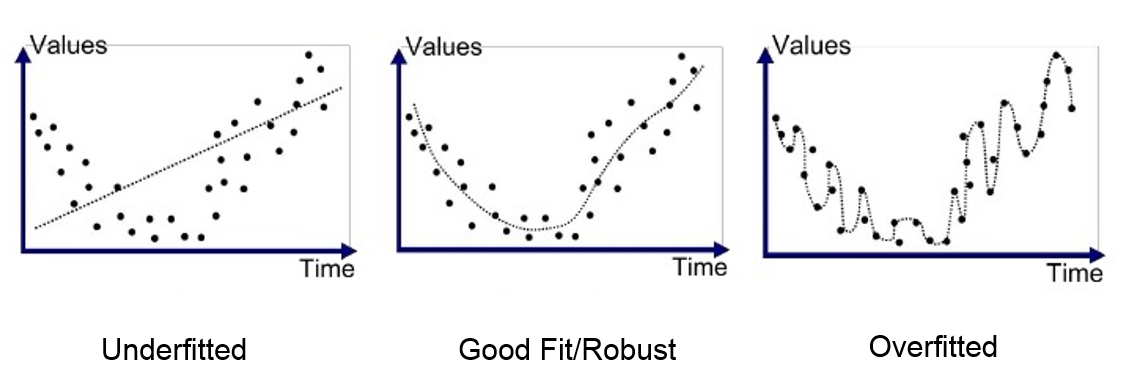
해당 그림은 파란색 점들이 있을 때, 그 점을 표현하는 곡선을 추정하는 경우를 나타낸다.
첫 번째 그림은 직선으로 단순하게 추정하므로 얼핏봐도 오류가 많아보인다. 즉 underfitted 현상이다
세 번째 그림이 과적합을 나타내는 그림이며, 모든 점들을 그대로 오차 없이 추정하는 경우이다. training data에 대해서는 오차가 전혀 없겠지만, 새로운 test data가 주어지는 경우에는 엉터리 결과가 나올 수도 있다.
가운데 그림은 비록 오차가 있지만 새로운 데이터들이 와도 좋은 결과가 나올 수 있다.
그렇다면 overfitting 현상을 해결하는 방법은 뭐가 잇을까?
Step 2. 해결책
1) 데이터 셋 늘리기
가장 확실한 방법 중 하나는 training data 양을 늘리는 것이다. 그렇게 되면 모델 학습시 범위나 경우를 다양하게 학습할 수 있기 때문이다.
그러나 학습 데이터를 얻으려면 과정 속에서 시간과 비용이 필요하고 양이 많아지게 되면 결국 학습에 걸리는 시간이 늘어나는 문제도 존재한다.
2) Features 개수 줄이기
설명 변수가 많을 경우 과적합이 발생할 수 있다. 설명 변수(독립 변수)가 많으면 차원의 저주(The Curse of Dimentionality) 라는 현상이 발생한다.
차원의 저주는 설명 변수가 많으면 많을수록 데이터가 그래프에서 표현되는 범위가 넓어져서 관측 값들이 넓은 범위에 분포하게 된다.
이 점들이 연결이 되면 노이즈가 발생하게 되는데 모델이 해당 노이즈를 결과로 나타낼 수 있어서 Overfitting이 발생할 가능성이 존재한다.
그래서 model selection algorithm을 사용하여 주요 feature들을 선택한다.
3) 가중치 Regularization(규제)
Feature의 개수를 많이 가지는 복잡한 모델은 간단한 모델보다 과적합될 가능성이 높다. 위에서 쓰인 feature를 버리는 방법이 아닌 가중치 규제(Regularization) 이 있다.
- L1 Norm : 가중치 w들의 절대값의 합계를 cost function에 추가
- L2 Norm : 가중치 w들의 제곱합을 cost function에 추가
위 공식에서 나오는 $λ$는 가중치 규제의 강도를 정하는 hypherparameter이다.
위 두 식 모두 비용 함수를 최소화하기 위해서 가중치 w들의 값이 작아져야한다는 특징을 가지고 있다. 그렇담 L1과 L2의 차이는 무엇일까?
L1을 사용하면 비용 함수가 최소화 되게하는 가중치를 찾는 동시에 가중치들의 절대값의 합도 최소가 되어야하므로 어떤 가중치 $w$의 값은 0에 가까워지거나 0이 될 수 있다. 그 말은 어떤 feature들은 모델을 만들 때 사용되지 않게 된다.
예를 들어 $H(x) = w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3} + w_{4}x_{4}$ 라는 수식이 있을 때, L1 를 사용해보자.
해당 결과 $w_3$의 값이 0이 되었다면, $x_3$ features는 모델을 만드는데 사용이 안된다.
그러나 L2는 L1과 달리 가중치가 완전히 0이 되기보다는 0에 가까워지는 경향을 확인 할 수 있다.
그럼 어느 경우에 L1을 쓰고, L2를 써야할까?
L1 norm은 어떤 feature들이 모델에 영향을 주고 있는지를 정확하게 판단하고자 할때 유용하고, 그렇지 않은 경우엔 L2 norm의 결과가 안정적이고 더욱 정확한 경우가 많다.
| L2 norm | L1 norm |
|---|---|
| Not very robust | Robust |
| Stable solution | Unstable solution |
| Always one solution | Multiple solution |
마지막으로 Regularization의 전후 그래프로 표현해보자.
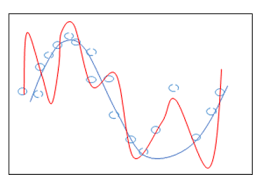
빨간색 선은 regularization 전의 overfitting된 결과이고, 파란색 선은 regularization 후의 결과이다.
즉, 각 feature의 weight의 크기 규제함으로써 overffiting의 현상을 해결할 수 있다.
참고자료
[https://wikidocs.net/35476] [http://hleecaster.com/ml-linear-regression-concept/] https://yongku.tistory.com/entry/%EB%94%A5%EB%9F%AC%EB%8B%9D%EA%B3%BC-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EA%B3%BC%EC%A0%81%ED%95%A9Overfitting-%EA%B3%BC%EC%A0%81%ED%95%A9Overfitting-%ED%99%95%EC%9D%B8%ED%95%B4%EB%B3%B4%EA%B8%B0 https://m.blog.naver.com/laonple/220522735677 https://towardsdatascience.com/topographic-regularized-feature-learning-in-tensorflow-manual-backprop-in-tf-f50507e69472